Masters Thesis part I : Inertial effects on heat or mass transfer from drops
This is a brief description of my Master's research which constitutes the first part of my MS thesis.
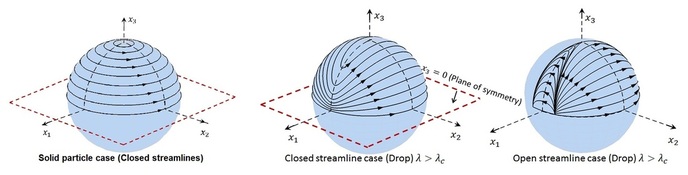
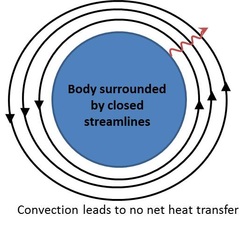
The main objective of this work is to establish the fundamental transport processes concerning heat or mass transfer from a dispersed phase (drops) to an ambient dispersing medium. Such transport processes are found in a large number of real world systems, for instance in chemical industries and evaporation of fuel droplets in combustion. Our approach involves asymptotic analysis and a boundary-layer type solution in a non-orthogonal coordinate system. We have established that even a small amount of inertia plays a significant role in the transport of heat or mass from a drop. The problem for drops presents several interesting features as compared to the analogous problem for solid particles. There are two regimes for the flow around a drop in a linear flow (1) open streamline regime and (2) closed streamline regime. We show that in the open streamline regime inertia plays only a sub-dominant role at leading order. We go on to solve the open streamline heat transfer problem making novel use of a classic non-orthogonal coordinate system. The closed streamline region around an object prevents effective transport of heat leading to diffusion limited transport (see picture inset). It is found that in the closed streamline regime inertia breaks the degeneracy of the closed streamlines and thereby plays a dominant role in the transport. The effect of inertia is to cause the previously closed streamlines to spiral away from the drop leading to a significant increase in heat transfer. In both cases we derive correlations for the Nusselt number which are expected to provide a useful theoretical basis for the ubiquitous problem of heat transfer from liquid dispersed phases.
The main objective of this work is to establish the fundamental transport processes concerning heat or mass transfer from a dispersed phase (drops) to an ambient dispersing medium. Such transport processes are found in a large number of real world systems, for instance in chemical industries and evaporation of fuel droplets in combustion. Our approach involves asymptotic analysis and a boundary-layer type solution in a non-orthogonal coordinate system. We have established that even a small amount of inertia plays a significant role in the transport of heat or mass from a drop. The problem for drops presents several interesting features as compared to the analogous problem for solid particles. There are two regimes for the flow around a drop in a linear flow (1) open streamline regime and (2) closed streamline regime. We show that in the open streamline regime inertia plays only a sub-dominant role at leading order. We go on to solve the open streamline heat transfer problem making novel use of a classic non-orthogonal coordinate system. The closed streamline region around an object prevents effective transport of heat leading to diffusion limited transport (see picture inset). It is found that in the closed streamline regime inertia breaks the degeneracy of the closed streamlines and thereby plays a dominant role in the transport. The effect of inertia is to cause the previously closed streamlines to spiral away from the drop leading to a significant increase in heat transfer. In both cases we derive correlations for the Nusselt number which are expected to provide a useful theoretical basis for the ubiquitous problem of heat transfer from liquid dispersed phases.